Phần 1: Tổng quan về mô hình SVM
Giới thiệu
Mô hình Support Vector Machine - SVM là một mô hình máy học thuộc nhóm Supervised Learning được sử dụng cho các bài toán Classification (Phân lớp) và Regression (Hồi quy).
Ta còn có thể phân loại mô hình này vào loại mô hình Tuyến tính (Linear Model), loại này bao gồm các thuật toán có chung một dạng hypothesis function (có thể gọi là Hàm giả định, tóm lại là cách nó đưa ra một dự đoán - prediction) có dạng là những đường thẳng (trong không gian 2 chiều), mặt phẳng, siêu phẳng (trong không gian nhiều chiều). Chúng ta cùng nhau thử nói sơ lược lại các mô hình Tuyến tính này.
Sơ lược các mô hình tuyến tính khác
Mô hình tuyến tính quan trọng nhất mà ai học qua Machine Learning đều biết là Linear Regression (Hồi quy tuyến tính). Sơ lược về mô hình này là tìm một đường thẳng khớp nhất với các điểm dữ liệu, để nắm bắt được xu hướng, mỗi tương quan, … của dữ liệu.
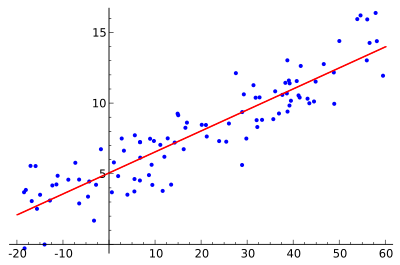
Như trong hình trên, hypothesis function của Linear Regression là một đường thẳng có dạng $y = w^Tx + b$.
Một mô hình tuyến tính khác dùng cho bài toán Classification nổi tiếng là Logistic Regression (Hồi quy logistic). Mặc dù dạng hypothesis function của nó là một đường cong, sau khi biến đổi bằng hàm phi tuyến sigmoid, nhưng bản chất của nó vẫn là một mô hình tuyến tính, hàm sigmoid là một hàm phi tuyến mang ý nghĩa biến đổi các giá trị liên tục thành những giá trị xác suất. Mô hình Logistic Regression có hypothesis function dạng $y = sigmoid(w^Tx + b)$.
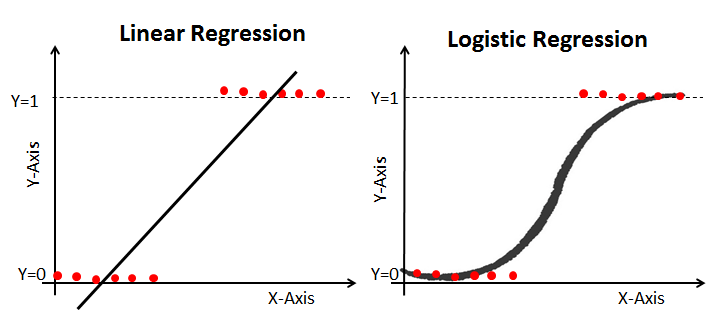
Nền tảng của mô hình SVM
Mô hình SVM đặt ra vấn đề giải quyết 1 bài toán đơn giản nhất là phân lớp 2 lớp dữ liệu. Với một tập dữ liệu sơ khởi nhất gồm 2 lớp được tách rõ rệt với nhau, vậy ta nên chọn đường nào có khả năng tổng quát cao nhất ?
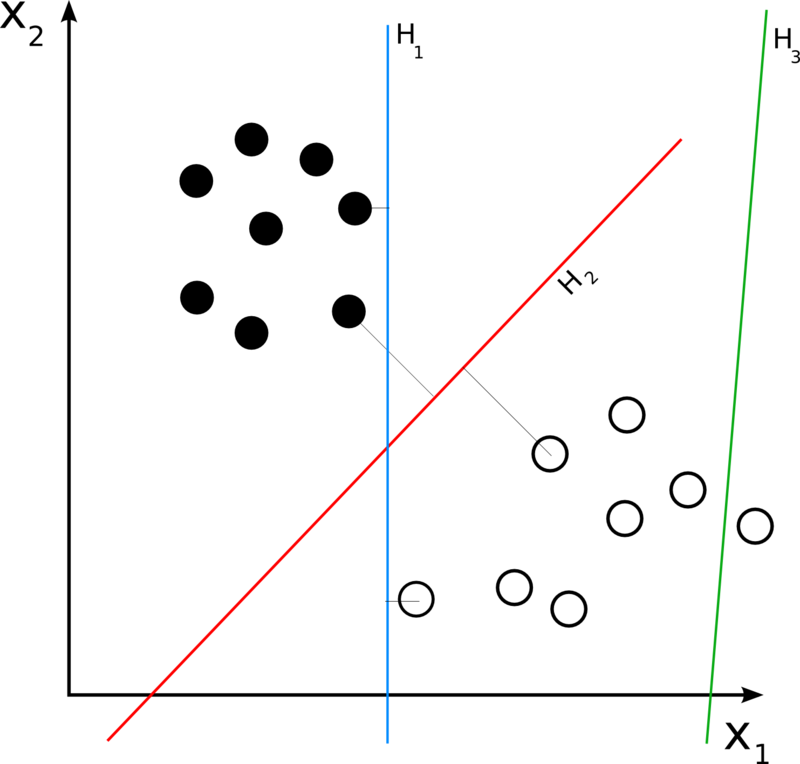
Tác giả của mô hình SVM là Vladimir Vapnik cho rằng “đường thẳng phân tách 2 lớp dữ liệu cách đều lớn nhất sẽ cho ra khả năng tổng quát tốt nhất”. Chúng ta gọi khoảng cách đều đó là margin (lề). Như trong ví dụ trên, đường thẳng H2 sẽ là đường thẳng tốt nhất mà ta có thể chọn được để phân tách 2 lớp. Vậy nên mô hình SVM chỉ có ý tưởng cơ bản như vậy tìm đường thẳng margin lớn nhất.
Tiêp theo, nếu mọi người tự tin vào việc đọc những công thức toán học, hãy tiếp tục phần 2, nếu không hãy tìm xuống phần kết luận cuối cùng về mô hình SVM :^)
Phát biểu bài toán cho mô hình SVM
Input: Bộ dữ liệu gồm 2 lớp
Output: Một đường thẳng phân cách 2 lớp với khoảng cách từ đường thẳng đó tới điểm gần nhất của từng lớp, là lớn nhất có thể.
Lý thuyết toán học
Đây là phần mình sẽ tóm tắt lại lý thuyết toán để tìm ra đường thẳng tối ưu của SVM. Các bạn nếu ngại đọc các phần chứng minh toán có thể kéo thẳng xuống phần Kết luận tóm tắt giải thuật.
Tập Hypothesis của SVM:
Tập Hypothesis của SVM có dạng:
\[y = h(x) = sign(w^Tx + b) ~~~~ (1)\]Với $x \in \mathbb{R}^d, w \in \mathbb{R}^d, b \in \mathbb{R}$, ta có $x$ là bộ dữ liệu trong không gian $d$ chiều và $w, b$ là các tham số về siêu phẳng trong không gian để phân tách.
Ngoài ra $sign(x)$ là một hàm xác định dấu, nếu $x >= 0$ $sign(x) = 1)$ ngược lại nếu $x < 0$ $sign(x) = -1$. Đây là cách phân lớp của từng điểm dữ liệu $y \in {-1, +1}$.
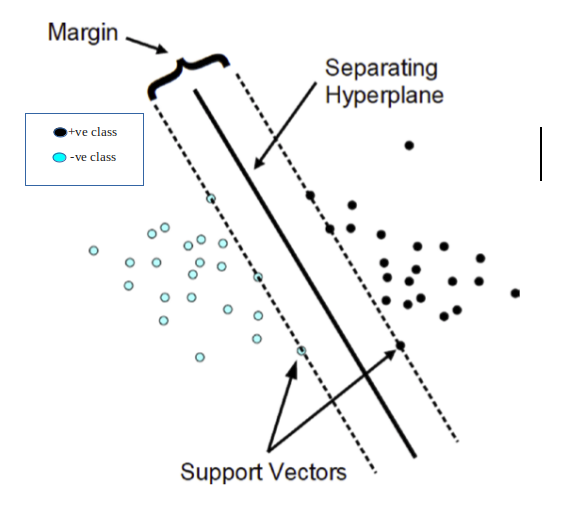
Bài toán tối ưu của SVM
Mục tiêu chính của SVM là tìm ra một mặt phẳng, chia tách 2 phần dữ liệu với “lề” (margin) lớn nhất.
Ta có bài toán tối ưu:
Gọi những $x_n$ là những điểm dữ liệu gần nhất với mặt phẳng $w^Tx + b$. Với kiến thức hình học cấp 3, ta dễ dàng tính được khoảng cách từ $x_n$ tới mặt phẳng là:
\[\frac{|w^T x_n + b|}{||w||_2} ~~~~ (2)\]Với
\[||w||_2 = \sqrt{\sum_{i=1}^d w_i^2}\]Để thuận tiện cho việc tính toán, sẽ normalize lại vector $w$ sao cho:
\[|w^Tx_n + b| = 1 ~~~~ (3)\]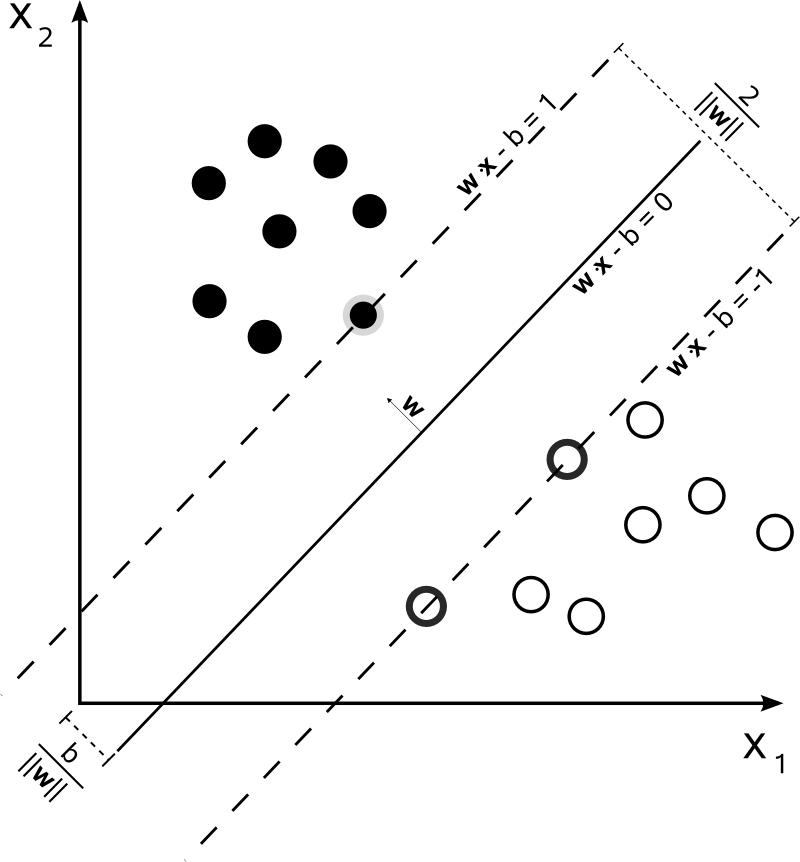
Từ đây ta có 2 nhận xét:
-
Những điểm $x_n$ được phân vào lớp $+1$ đều có giá trị $w^Tx + b \geq 1$, tương tự nếu được phân vào lớp $-1$, giá trị $w^Tx + b \leq -1$. Đây chính là cách phân lớp cho các điểm dữ liệu sau khi normalize $w$. Đặt $N$ là số lượng điểm dữ liệu, ta có $y_n(w^Tx_n +b) >= 1$ $\forall n=1, 2, 3 … N$
-
Độ lớn của “lề” lớn nhất cho một mặt phẳng $w^Tx + b$ là
Ta phát biểu bài toán tối ưu cho SVM như sau:
\[\text{maximize } \frac{2}{||w||_2}\] \[\text{subject to } y_n(w^Tx_n +b) >= 1 \forall n=1, 2, 3 ... N\]Hay ta có thể viết lại bài toán trên thành:
\(\text{minimize } \frac{1}{2} w^Tw\) \(~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(4)\) \(\text{subject to } y_n(w^Tx_n +b) >= 1 \text{ }\forall n=1, 2, 3 ... N\)
Phương pháp tối ưu cho SVM:
Từ đây chúng ta thấy áp dụng phương pháp nhân tử Lagrange (đã được học trong Giải tích 1) (đọc lại phương pháp nhân tử Lagrange để tìm cực trị ở đây) với ràng buộc bất đẳng thức:
\[\mathcal{L}(w, b, \alpha) = \frac{1}{2} w^Tw - \sum_{n=1}^N \alpha_n(y_n(w^Tx_n + b) - 1)\] \[(4) \Leftrightarrow \text{Minimize with } w, b; \text{Maximize with } \alpha:\alpha_n \geq 0 \text{ } \mathcal{L}(w, b, \alpha) ~~~~ (*)\]Nhìn chung đây là bài toán tối ưu từ dạng primal form cho bài toán (4) thành dạng dual form (đối ngẫu với min, max) của bài toán (*).
Để giải bài toán (*), ta có thể giải lần lượt từ Maximize cho $w, b$ khi coi các $\alpha_n$ là hằng số; tiếp theo là giải Minimize với $\alpha_n \geq 0$ coi $w, b$ là hằng số. Mặc dù cách giải này sẽ cần một số điều kiện để tối ưu, nhưng trong phạm vi bài giới thiệu chúng sẽ tạm thời được lược bỏ (nếu mọi người vẫn muốn đọc các phần chứng minh và điều kiện tối ưu tham khảo tại đây).
Minimize with $w, b$
Minimize $\mathcal{L}(w, b, \alpha) = \frac{1}{2} w^Tw - \sum_{n=1}^N \alpha_n(y_n(w^Tx_n + b) - 1)$ with $w, b$
Lấy đạo hàm của $w, b$ và đặt đạo hàm bằng 0, ta có:
\[\frac{\partial \mathcal{L}}{\partial w} = w - \sum_{n=1}^N \alpha_n y_n x_n = 0 \Leftrightarrow w = \sum_{n=1}^N \alpha_n y_n x_n ~~~~ (5)\] \[\frac{\partial \mathcal{L}}{\partial b} = - \sum_{n=1}^N \alpha_n y_n = 0 \Leftrightarrow \sum_{n=1}^N \alpha_n y_n = 0 ~~~~ (6)\]Thay thế (5) và (6) vào $\mathcal{L}(w, b, \alpha)$ và rút gọn, ta có:
\[\mathcal{L}(\alpha) = \sum_{n=1}^N \alpha_n - \frac{1}{2} \sum_{n=1}^N \sum_{m=1}^M y_n y_m \alpha_n \alpha_m x_n^T x_m\]Vậy bài toán tối ưu ta chỉ còn lại:
\[\text{Maximize } \mathcal{L}(\alpha) = \sum_{n=1}^N \alpha_n - \frac{1}{2} \sum_{n=1}^N \sum_{m=1}^M y_n y_m \alpha_n \alpha_m x_n^T x_m ~~~ (**)\]Với các $\alpha_n \geq 0$ với mọi $n = 1,2, … N$, cộng thêm ràng buộc từ (6) $\sum_{n=1}^N \alpha_n y_n = 0$
Vậy từ một dạng primal form (4), ta đã chuyển về dạng dual form như bài toán (*), và cuối cùng ta chỉ cần tìm ra các nghiệm $\alpha_n$ để hoàn thành quá trình tối ưu cho SVM.
Việc tìm ra các $\alpha_n$ sẽ sử dụng Quadratic Programming (QP - dịch là quy hoạch toàn phương) để giải ra. Vậy nên ta có thể tóm tắt lại các bước của việc tối ưu cho SVM như sau:
- Giải các nghiệm $\alpha_n$ thoả:
Với các $\alpha_n \geq 0$ và $\sum_{n=1}^N \alpha_n y_n = 0$
- Từ các $\alpha_n$, ta tính được $w$ theo (5):
Một chú ý khi giải các $\alpha_n$, thực tế khi giải ra bằng QP chỉ có một số $\alpha_n > 0$, nên ta có thể viết lại: $w = \sum_{\alpha_n > 0} \alpha_n y_n x_n$
Mặt khác, với những $\alpha_n > 0$, ta lại có $\alpha_n (y_n(w^T + b) - 1) = 0$ (Từ một trong những điều kiện Karush-Kuhn-Tucker - KKT để chuyển từ dạng primal form thành dual form), suy ra: $y_n(w^T + b) = 1$.
Từ nhận xét này, ta có thể khẳng định những điểm $x_n$ có các $\alpha_n > 0$ tương ứng là những điểm nằm gần nhất với mặt phẳng $w^Tx + b$ và có khoảng cách tới mặt phẳng là
\[\frac{1}{||w||_2}\]Chúng đóng góp vào việc tính toán ra vector pháp tuyến $w$ của mặt phẳng, vậy nên ta gọi những điểm $x_n$ đó là những support vector.
- Tìm hệ số $b$. Ta có thể tìm hệ số $b$ bằng cách dùng bất kì support vector nào vì $y_n(w^T x_n + b) = 1$.
Kết luận chung bài toán SVM
-
Vì sao gọi là Support Vector Machine ? Vì mô hình này được xây dựng dựa trên việc tìm ra các điểm $x_n$ đóng góp vào việc tìm ra mặt phẳng phân tách dữ liệu bài toán, cụ thể hoá bằng việc giải ra bài toán tối ưu với những $\alpha_n$ tương ứng $x_n$ ta đã chứng minh ở trên.
-
Khả năng tổng quát của mô hình SVM như thế nào ? Đây chính là một kết quả được đánh giá từ những phân tích thực tế. Người ta thấy rằng mô hình càng cho ra ít support vector thì khả năng tổng quát càng tốt. Kết quả tổng quát được tóm tắt với biểu thức sau:
\[\mathop{\mathbb{E}}[Error_{out}] \leq \frac{\mathop{\mathbb{E}}[\text{\#SV}]}{N - 1}\]Nhìn chung người ta luôn kì vọng vào việc tìm ra thật ít Support Vector để làm giảm cận trên của độ lỗi trong thực tế ($Error_{out}$). Nếu có dữ liệu 1000 điểm, bạn tìm ra được khoảng 10 support vector, thì mô hình của bạn khá là tốt :)
-
Ưu điểm của SVM: Nhìn chung đây là một mô hình có ý tưởng đơn giản, có khả năng giải thích bằng toán học và tìm ra tính tổng quát của mô hình rất thuận lợi. Tính tổng quát của mô hình có thể được áp dụng trong thực tế với dữ liệu nhiều chiều và phức tạp. Những cách tối ưu này sẽ được giới thiệu trong phần sau.
-
Nhược điểm của SVM: Mô hình SVM dựa trên bài toán tối ưu bằng Quadratic Programming, nhìn chung đây là bài toán tối ưu với chi phí rất tốn kém, trong trường hợp các vector $x_n$ càng nhiều chiều, hoặc số điểm dữ liệu $N$ càng lớn cũng tốn rất nhiều thời gian.



Leave a comment