Phần 2: Áp dụng mô hình SVM trong thực tế
Dữ liệu không khả tách tuyến tính:
Trước tiên chúng ta có định nghĩa về linear separability (tính khả tách tuyến tính) của dữ liệụ. Một dữ liệu được coi là khả tách tuyến tính khi chúng ta có thể dùng một đường thẳng để phân tách 2 lớp của nó rõ rệt, như hình sau:
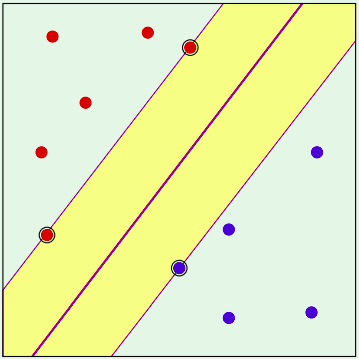
Mô hình SVM được xây dựng dựa trên tiêu chí ban đầu sơ khởi cho dữ liệu như này, tuy nhiên đời không như là mơ thực tế các dữ liệu không có khả năng tách bằng một đường thẳng như vậy, ví dụ như các trường hợp:
- Trường hợp 1: Dữ liệu không thể tách ra bằng 1 đường thẳng
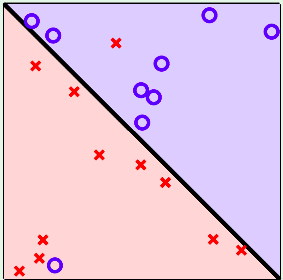
- Trường hợp 2: Dữ liệu là phi tuyến tính
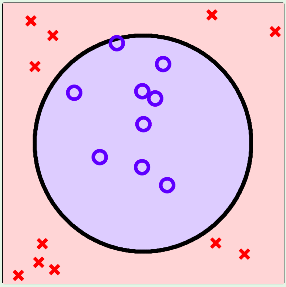
Mô hình SVM có những công cụ để áp dụng cho các trường hợp dữ liệu như thế này bao gồm 2 phương pháp chính: Biến đổi phi tuyến với Kernel, Soft-Margin (Lề mềm).
Biến đổi phi tuyến với các Kernel:
Đây là phương pháp được áp dụng cho các dữ liệu phi tuyến, ta xét ví dụ sau:
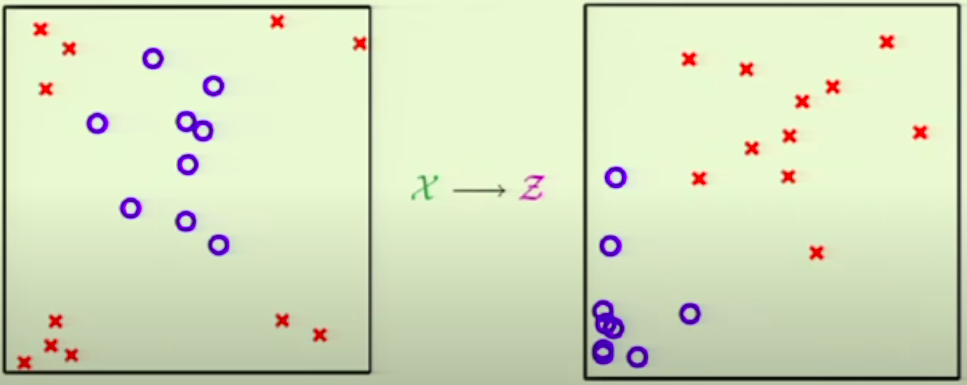
Với hình bên trái với dữ liệu trong không gian $\mathbf{X}$, ta không thể áp dụng bất kì đường thẳng SVM nào để phân tách 2 phần dữ liệu.
Với hình bên phải là không gian được biến đổi phi tuyến từ $X$ bằng việc điều chỉnh lại gốc toạ độ ở tâm hình ảnh và áp dụng ánh xạ từ $(x_1, x_2) \in \mathbf{X} \longrightarrow (x_1^2, x_2^2) \in \mathbf{Z}$
Từ đó ta có thể áp dụng SVM một cách đơn giản trên không gian được biến đổi $\mathbf{Z}$.
Với mô hình SVM, ta không cần phải áp dụng các phép biến đổi phi tuyến trực tiếp lên từng điểm dữ liệu, vì dựa vào bài toán tối ưu ta có:
\[\underset{\alpha}{\operatorname{argmin}} \frac{1}{2} \sum_{n=1}^N \sum_{m=1}^N y_n y_m \alpha_n \alpha_m x_n^T x_m - \sum_{n=1}^N \alpha_n\]Ở trong bài toán tối ưu này, ta chỉ cần quan tâm vào tích vô hướng của 2 điểm dữ liệu bất kì $x_n^T x_m$ để tạo ra ma trận Quadratic cho bài toán giải Quadratic Programming để tìm ra $\alpha_n$.
Vậy khi ta cần áp dụng một phép biến đổi $z = \Phi(x)$ vào cho không gian dữ liệu $\mathbf{X}$ để tạo không gian dữ liệu $\mathbf{Z}$, ta chỉ cần định nghĩa một hàm $K(x, x’) = \Phi(x)^T \Phi(x’) = z^T z’$
Từ đây bài toán tối ưu của chúng ta chỉ cần thay đổi một chút thành:
\[\underset{\alpha}{\operatorname{argmin}} \frac{1}{2} \sum_{n=1}^N \sum_{m=1}^N y_n y_m \alpha_n \alpha_m K(x_n, x_m) - \sum_{n=1}^N \alpha_n\]Hàm $K$ sẽ được gọi là hàm Kernel cho mô hình SVM. Một số hàm Kernel thường được sử dụng cho SVM như sau:
- $K(x, x’) = x^T x’$ Đây là hàm Kernel tuyến tính ban đầu của SVM.
- $K(x, x’) = (a(x^T x’) + b)^Q$ Đây là hàm kernel đa thức (polynomial) với $Q$ là bậc của đa thức, $a, b$ là các hệ số.
- $K(x, x’) = exp(- \gamma |x - x’|^2)$. Đây là một hàm kernel có vô hạn chiều được gọi là hàm RBF - Radial Bias Function. Chứng minh cho phép biến đổi thành không gian vô hạn chiều này được tóm tắt tại đây
Mô hình SVM với Lề mềm (Soft-margin):
Với mô hình SVM gốc chúng ta đã bàn ở trên, được gọi là mô hình SVM Lề cứng (SVM Hard-margin), với tập hypothesis $h(x)$ và độ lớn margin được tính từ các support vector $x_n$ thỏa mãn ràng buộc là $y_n(w^T x_n +b) = 1$. Hay chúng ta có thể viết một cách tổng quát hơn cho mọi điểm trong tập dữ liệu $y_n(w^T x_n + b) \geq 1, n=1,2,3 … N$.
Trong nhiều trường hợp, mô hình Hard-margin quá khó để đáp ứng khi chúng ta đưa ra điều kiện quá khó để đáp ứng, cũng như các độ nhiễu trong các tập dữ liệu, chúng ta thường muốn 1 cơ chế tìm đường thẳng phân tách dữ liệu và lề dễ dàng hơn, từ đó mô hình SVM Soft-margin được tạo ra. Ta gọi $\xi_n$ là một tham số vi phạm tương ứng với mỗi điểm $x_n$, SVM Soft-margin chỉ yêu cầu điều kiện $y_n(w^T x_n + b) \geq 1 - \xi_n$ với $\xi_n \geq 0$.
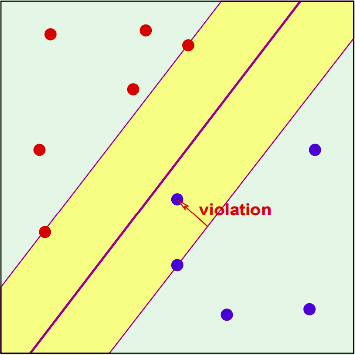
Ta sẽ mô hình hóa lại việc các điểm dữ liệu “được phép vi phạm” ràng buộc $y_n(w^T x_n + b) \geq 1, n=1,2,3 … N$ như sau:
Với $\xi_n \geq 0$ là các tham số vi phạm tương ứng với mỗi điểm dữ liệu $x_n$, ta cần thỏa mãn: $y_n(w^T x_n + b) \geq 1 - \xi_n$.
Tổng giá trị vi phạm là $\sum_{n=1}^N \xi_n$.
Bài toán tối ưu được viết lại từ (4) thành:
\(\text{minimize } \frac{1}{2} w^Tw + C\sum_{n=1}^N \xi_n\) \(~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(6)\) \(\text{subject to } y_n(w^Tx_n +b) >= 1 - \xi_n, \xi_n \geq 0 \text{ }\forall n=1, 2, 3 ... N\)
Giải thích thêm vì sao lại thêm đai lượng $C\sum_{n=1}^N \xi_n$, chúng ta đang cực tiểu hóa $\frac{1}{2} w^Tw$ tương đương với việc cực đại hóa độ lớn của lề.
Đại lượng $\sum_{n=1}^N \xi_n$ thể hiện cho mức độ sự vi phạm độ lớn của lề, $C$ là một tham số thể hiện tương quan giữa 2 mục tiêu tối ưu.
Một cách hơi suy đoán, chúng ta sẽ cảm giác thấy $C\sum_{n=1}^N \xi_n$ gần giống như Regularization cho mô hình SVM, và thực tế chúng ta sẽ chứng minh sau đây:
Ta có hàm nhân tử Lagrange tương ứng với giải bài toán (6) là:
\[\mathcal{L}(w, b, \xi, \alpha, \beta) = \frac{1}{2} w^Tw + C\sum_{n=1}^N \xi_n - \sum_{n=1}^N \alpha_n(y_n(w^Tx_n + b) - 1) - \sum_{n=1}^N \beta_n \xi_n\]Hàm $\mathcal{L}$ cần minimize với $w, b, \xi$, và maximize với mọi $\alpha_n \geq 0$ và $\beta_n \geq 0$.
Tiếp tục giải ra bài toán này như trên, ta sẽ đưa ra các kết quả gần tương tự với SVM Hard-margin:
\[\frac{\partial \mathcal{L}}{\partial w} = w - \sum_{n=1}^N \alpha_n x_n y_n = 0\] \[\frac{\partial \mathcal{L}}{\partial b} = -\sum_{n=1}^N \alpha_n y_n = 0\]Thêm vào đó:
\[\frac{\partial \mathcal{L}}{\partial \xi_n} = C - \alpha_n - \beta_n = 0 ~~~~(7)\]Tiếp tục thay thế các kết quả trên vào bài toán tối ưu cho các $\alpha$, ta có:
\[Maximize \mathcal{L}(\alpha) = \sum_{n=1}^N \alpha_n - \frac{1}{2} \sum_{n=1}^N \sum_{m=1}^M y_n y_m \alpha_n \alpha_m x_n^T x_m\]Với $0 \leq \alpha_n \leq C$ (được suy ra từ (7)) với mọi $n=1,2,3 … N$ và $\sum_{n=1}^N \alpha_n y_n = 0$
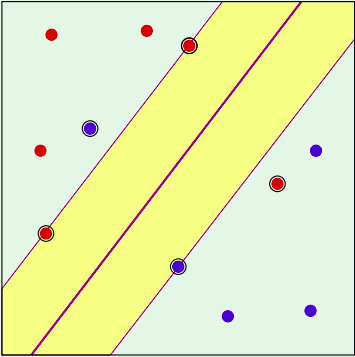
Tiếp tục giải bài toán trên bằng QP và việc ta có 1 giới hạn cho nhưng $\alpha_n$ được suy ra từ (7), với mỗi $x_n$ là những support vector được tìm ra sẽ có các giá trị $\alpha_n$ tương ứng được giới hạn $0 \leq \alpha_n \leq C$. Nhưng ta vẫn sẽ phân chia các support vector vào 2 loại:
- Với những support vector $x_n$ có $\alpha_n < C$, ta gọi chúng là những margin support vector (những support vector nằm trên lề) vì $\alpha_n < C \Rightarrow \beta_n > 0 \Rightarrow \xi_n = 0$ (để thỏa mãn cho bài toán maximize ở trên).
Đây chính là những vector thỏa mãn ràng buộc $y_n(w^T x_n + b) = 1$.
- Với những support vector $x_n$ có $\alpha_n = C$, ta gọi chúng là những non-margin support vector (support vector không nằm trên lề): $\alpha_n = C \Rightarrow \xi_n > 0$.
Các support vector này có tính chất $y_n(w^T x_n + b) < 1$.
Tổng kết về SVM trong thực tế
Vai trò của các hàm Kernel:
Các hàm kernel áp dụng cho SVM là cách đơn giản nhất để áp dụng các phép biến đổi phi tuyến vào dữ liệu, mà không cần phải trực tiếp biến đổi dữ liệu đầu vào. Các hàm kernel khác nhau cũng có độ phức tạp khác nhau, cụ thể là độ phức tạp của linear kernel < polynomial kernel < rbf kernel.
Việc áp dụng kernel nào cũng đòi hỏi 1 số bước đánh giá về dữ liệu và có chút “kinh nghiệm” để áp dụng cho phù hợp.
Vai trò của tham số C trong Soft-margin:
Đây là tham số mà mọi người dùng SVM đều muốn tìm kiếm. Mình sẽ tổng kết tham số C qua các kết luận sau:
-
$C$ thể hiện cho sự đánh đổi trong việc tối đa hóa độ lớn của lề với việc làm cho độ lỗi của mô hình thật nhỏ. Với Hard-margin, độ lỗi của mô hình sẽ rất nhỏ lúc huấn luyện, nhưng độ lớn của lề rất nhỏ dẫn tới việc tổng quát hóa có thể bị ảnh hưởng, nên chúng ta thường muốn nới lỏng bằng Soft-margin để tăng độ lớn của lề lên và chấp nhận độ lỗi lúc huấn luyện có thể cao hơn.
-
$C$ đóng vai trò gần tương tư như Regularization cho SVM.
-
Khi điều chỉnh tham số C, ta cần chú ý: với giá trị C càng tăng lên, nghĩa là các non-margin support vector $x_n$ càng khó khăn đạt được giá trị $\alpha_n = C$, mô hình sẽ chuyển từ Soft-margin thành Hard-margin, độ lớn của lề khi tìm được sẽ nhỏ lại. Với các giá trị $C$ càng nhỏ dần, nghĩa là ta sẽ chấp nhận nhiều non-margin support vector hơn, độ lớn của lề sẽ tăng lên.
Các bước áp dụng
Trong thực tế nếu muốn áp dụng SVM, chúng ta cần sử dụng phối hợp nhiều tham số khác nhau cho việc Biến đổi phi tuyến và sử dụng Lề mềm. Sau đây là một số bước khi áp dụng cho SVM.
-
Phân tích dữ liệu, tương quan giữa các đặc trưng, tìm các kernel để áp dụng cho việc biến đổi phi tuyến, có thể cân nhắc kernel đa thức, kernel RBF. Thử tìm ra các tham số phù hợp cho các kernel cụ thể.
-
Áp dụng lề mềm cho cac mô hình sử dụng kernel khác nhau với các tham số C, mặc định là 1.0, cân nhắc tham số C này trong các giá trị 0.01, 0.1, 1, 10, 100.
-
Có thể gridsearch để tìm ra tham số tối ưu của các kernel và các tham số liên quan khác.



Leave a comment